In the previous article, we looked at how positions of any kind form an affine space, whose differences are vectors. For when we are dealing with scalar quantities, in this final part of the series, we look for a more lightweight mathematical structure. As mentioned earlier, we use real numbers as values for things like temperature, but we can’t bring over all the familiar operations like addition (that they satisfy due to their field structure) to our physical quantities.
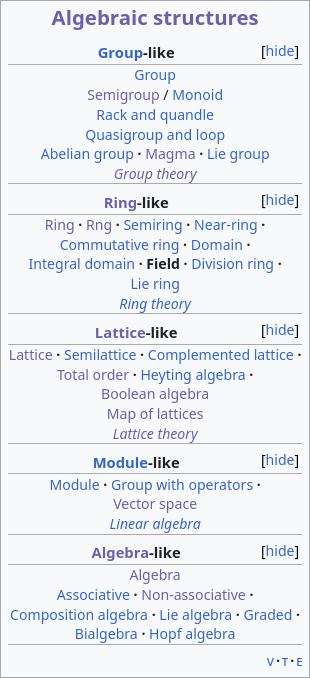
Well algebra has no shortage of mathematical structures with and without strange esoteric properties. But its surprisingly hard to track down a suitable mathematical answer from vector spaces or fields even if you knew what you were looking for. And it isn’t wiki’s fault either, they’ve got this nice little box (snapshot below) organising many related entities titled Algebraic Structures. Expanding all the ‘[show]’s however gets you no closer (see below).
The dive
The way algebra works is that there are many structures where sets are tied up with operations and axioms are attached to these structures. Each structure then becomes a full-blown topic for study in its own right, like groups (you’d have encountered this in school likely), rings, fields, vector spaces, Banach spaces, Hilbert spaces, and more, forming a dizzying array of entities. Fields are a relatively specialised structure with a lot of axioms and being closed under two different operations. So let’s start dropping axioms and operations from fields till we get to something useful, shall we?
A field is listed under ‘ring-like’ structures in that box. The least restrictive structure in that section is the cheekily named rng, a set closed under addition and multiplication but without the equivalent of a × 1 = a that we take for granted. But addition is a no-go, so there’s more chopping required still. ‘Group-like’ looks more interesting because they only need one operation, and hopefully something there drops even that one operation? Modules and Algebras (yes they are a type of algebraic structures studied in the subject of abstract algebra, and yes I agree they really needed to choose a different name) have even more structure and axioms piled on on top of fields (modules are almost vector spaces in fact), so they’re an immediate no-go.
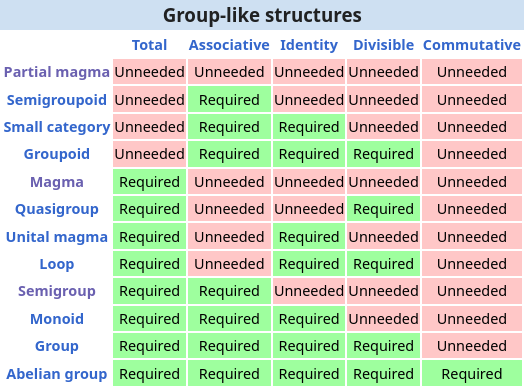
And while group-like certainly delivers on the less axioms bit (see above, though only group-like structures get their own detailed table in the “Outline of algebraic structures”), they never drop the (usually thought of as addition) operation. E ven the exotic goopy-sounding “partial magma”, which is barely more than a set and allows a subset of elements to obey the (addition) operation, still needs an operation. And because the subtracting one position from another yields a displacement which is a genuine vector, that operation can’t be subtraction either. Downward we go then, abandoning even more order and structure as we descend into savagery sets.
Sets. Just collections of numbers, a way to tell if something is in them or isn’t … and in our case a total ordering since its pretty important to be able to compare temperatures. But we still need to be able to subtract and then work with the differences. So this feels a little bare.
Now for all the physical quantities we care about, we could do a little better by adding the notion of distance between any two numbers, to get a metric space. And this may have been barely sufficient, but for the fact that the distance has to be positive. And we haven’t even gotten to allowing the quantity differences to be added, subtracted, divided etc.
Torsors
But waitaminute, surely this has been done before? Why are we doing basic algebra research on an extremely straightforward property of our physical world? Fortunately, there is indeed prior (obscure) art on this.
So it turns out our elusive algebraic structures are called torsors – and its extremely likely you’re hearing about it for the first time in your life. So it turns out that dropping properties wasn’t going to lead us to much of anywhere. Instead the differences in values are happily treated as our ordinary numbers in blessedly-axiom-rich real number field. But the absolute values themselves just form a bare set which is just associated with this field. Torsors are also called principal homogenous spaces, where a homogenous space brings in the group action and the “principal” property implies a kind of linearity. In fact, it seems that affine spaces are in fact torsors where the group is a vector space.
Just like affine spaces, torsors are also defined as a set (call it Tabs for our temperature test-case) with a group action on it. Here, for our purposes, the group is the set (call it TΔ) of real numbers with the addition operation. Because these represent temperature differences, TΔ occupies the entire −∞ C° to +∞ C°. The set Tabs spans [−273 °C, +∞ °C), and the torsor properties guarantee that for any two absolute temperatures, there exists a temperature difference between them. The restriction that an invalid absolute temperature (absolute hot, anyone?) does not result from an arithmetic operation will have to be enforced in the definition of the group action.
That’s it! In one stroke, we have solved several niggling issues of how to represent these physical quantities. More examples:
- Voltage, or more accurately electric potential difference, is only ever defined between two points. An electric potential does indeed exist at each point but is undetermined and possibly unknowable by definition. Potential at points in Euclidean space are members of the set of reals, and potential differences would form the group/field of reals, and we only ever evaluate the differences but the calculations are based on electric fields at those points. Absolute potential is an ℝ-torsor.
- Time is a more valuable case given a pressing need for picking a zero but which is otherwise meaningless. Time instants are members of the set of reals, and time intervals are members of the group/field of positive reals. Time intervals naturally result as from subtracting one time instant from another. Timezones would be an interesting concept to model here, and perhaps is better off defined as a vector. Time is an ℝ⁺-torsor.
I have vivid memories of dealing with time programmatically where correct handling and distinctions between instants and intervals was what sold me on that particular software library.
Torsors also apply perfectly to memory pointers – the type of pointer could be embedded into the group action as a size parameter which ends up multiplying the offsets. A void pointer would then be a set with no group action at all, essentially hobbling the ability to do pointer arithmetic. Therefore, pointers are ℤ-torsors!
To summarise, we represent temperature with a real number and a unit, and we expect to add/subtract/multiply/divide with reals because the set of real numbers is usually tacked on with closure under addition and multiplication (called a field in algebra). However, with many physical quantities that doesn’t make sense, and we need a more restrictive algebraic structure than fields. In such quantities, the right way is to classify absolute temperature as a different type of object than temperature differences which are just numbers, and explicitly define addition between an absolute and a difference. This structure is called a torsor.
Diving deeper
This actually felt like a small book, phew. I’m also linking a couple of further good resources:
- This mathoverflow answer goes into the origin of the term
- Matt Baker’s alternate construction of proportion spaces is later shown by commenters to be equivalent to a heap.
- And finally Terence Tao (perhaps the greatest living mathematician) has written a beautiful piece on the ways to axiomatise physical units and dimension. He also mentions torsors for the same reason that I do (yay!).
The heap construction is also quite cleverly suited for the matter at hand, managing without the need for a separate set and group. Instead, it uses a single ternary operation (our usual arithmetic are all binary operations!) which more or less comes out to a−a+b, with some properties: given five elements of the heap, it satisfies the equivalent of a−a+b = b, and a−b+(c−d+e) = (a−b+c)−d+e . The elements are the same as the elements of the torsor itself, like absolute temperature, absolute potential, time instants, absolute pointer, etc. This very much does satisfy the restriction we need. The only reason I prefer the torsor construction is that it explicitly defines the differences/intervals as members of the group, which obviously have their own rightful existence.
Epilogue
I want to be clear here that there is no original work here, lest someone mistake so. I simply scoured the internet and am paraphrasing existing work targeted at the apparently-niche need of merely most physical parameters (!) I have been liberal in hyperlinking multiple good resources, because I needed all of them together to get the picture. I am not exactly a mathematician by training, let alone by profession, so I gladly welcome any corrections or discussions. I haven’t added a lot of mathematical notation here because I am not doing any rigorous work here and would not like to give anyone that idea. (Plus I’m hoping to add LaTeX capability to my blog another day). And if anyone liked the usage of some typographical symbols like degrees, sets, and the minus sign, I’ll be happier. Adiós, amig(o/a)s!