In the first part, I talked about intuitive reasons why some physical quantities can’t be subject to the full repertoire of math operations. There’s more fun to be had, however, in the mathematical aspects of this limitation for related quantities like position and pointers (which are not addable due to a closely related but distinct reason from that of temperature).

Let’s check out your room

Let’s ask a different but equally simple question as in the last part: why can’t we add positions in 3-D space (or 2-D space for that matter)?

By which I mean, if you fix any given point in your bedroom as your origin, and mark the positions of various objects as 3-tuples ( 𝑥^*,𝑦^*,𝑧^* ), it makes literally no sense to add the position of your unwashed-clothes-bearing-chair to that of your underused washbasket (with a caveat for later). It does make sense to subtract them though, which gives you the 3-tuple displacement between the two (which is pointing from your washbasket to your chair, if you’re keeping track). It is also probably congruent to too-far-to-move-stuff currently.

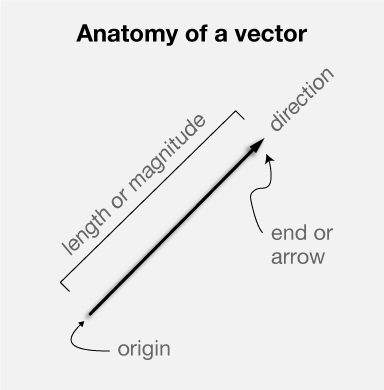
So now that we have brought in displacements, what can we say about them? Pretty straight: its a vector quantity, which just means it has a magnitude and direction. How to displacements differ from positions (after all both are 3-tuples)? The general answer on the internet is to distinguish between bound and free vectors. The terminology is fairly widespread in teaching material – I also encountered it, but none of us picked up on the distinctions involved and it never mattered. The biggest problem is that no one tells us what operations can be done on these bound and free vectors. Also, they tend to be emphasised in the definition, but eventually the distinction is lost (see here for e.g. towards the end, even though great care was taken initially) and any ordered sequence of 3 numbers become vectors. And then only intuition keeps calculations from becoming nonsensical. There’s more structure required for the bound vectors, so we have to go back to some definitions.

What’s a vector anyway?

Given the utter simplicity of the question for which apparently even STEM graduates can’t give the proper answer, let alone school teachers, we should probably be more rigorous than “a vector is a quantity with magnitude and direction”.

To do that, we first have to figure out what a scalar is. Again, the simple physics answer to this is a physical quantity (such as temperature) that can be represented only by magnitude (which is a number) with a unit. But merely being a number hasn’t told us whether certain scalars can be added or multiplied together. In math though, a scalar is a member of a field, which can be added, subtracted, multiplied, or divided by another (non-zero) scalar to yield another scalar. A very beautiful way of rewording this is that the field is closed under these four operations.

Building on this, a vector space over a scalar field is basically a set of sequences/tuples of scalars together with two binary operations: + (applies to two vectors and results in another vector), and × (applies between a scalar and a vector and results in another vector) that satisfy several axioms which I’ll not get into here. Among many others, the displacements between positions in your room that we talked about above can be added and multiplied/stretched by a scalar, and are clearly vectors.

Already, you can see that the vector space is also closed under addition, but multiplication of two vectors isn’t part of the deal.

This closure property makes a pretty powerful statement – that is, given any possible vectors and the addition operation, you have no hope of getting out of that vector space with any combination of operations. Sounds scary if you’re in a vector jail, but very satisfyingly safe if viruses were vectors. (Unfortunately, viruses are carried by a very different kind of vector nevertheless with suprising etymological commonality.) More to the point, closure is amazing if you’re trying to set boundaries or prove on what you can/can’t do with things and operations on those things. Same for velocities, accelerations, angular velocities, force, yada yada yada you get the drift.

But back to our position-addition-problem. The main reason I’m not going into vector space axioms is because they’re utterly irrelevant to what’s coming next. As we saw above, the scalars that vectors are defined using, come from a field. And a field is a set that is closed under addition, multiplication and their inverse operations (no prizes for guessing which they are). But the “scalars” of our positions, i.e. the underlying 𝑥-, 𝑦-, or 𝑧-components in the positions of your chair and washbasket, themselves don’t make sense to add (with the aforementioned caveat). And that’s not least because the result is nonsensically dependent on whether the origin is your room corner or the other side of the country. The components of position just can’t be meaningfully added, and thus don’t even begin to form a field.

Incidentally, we can now recognise that voltages and time, also “scalar” quantities in physics, do not form a field.

A familiar yet rigorous term

It turns out that geometry, only a little more rigorous than I learned in high school, always had the perfect answer to this issue of position arithmetic. It even has a very familiar sounding-name which pops in and out of common parlance and mathematical boilerplate setup. The concise answer is that positions in our real world belong to the Euclidean space. And Euclidean spaces in general are NOT vector spaces! Rather they are a very important type of structure called affine spaces. Affine spaces are sets whose members are called points (sounds familiar?), which are however associated with a vector space, and an action (we’re almost there). This action is a kind of function that does addition between a point and a vector to give… another point!

There are further technical conditions that successively add the expected intuitive properties of physical space onto the mathematical object. The Euclidean space also requires the presence of a dot product on its associated vector space, which doesn’t come built-in with a regular vector space.

One of these technical conditions essentially says that by fixing one particular point in the affine space as the origin, there must exist a corresponding vector for every point and vice versa. And this is the origin of the sloppy thinking that got us to this problem in the first place.

We were taught loosely that points were some kind of vectors, which some people call “bound vectors” or “position vectors”. The truth is the vectors from a given point in the affine space to each other point are displacement vectors or “free vectors”. And adding displacement vectors corresponding to two points is tantamount to marking a point with which you can complete a parallelogram. And that parallelogram is completely dependent upon what the origin is, and is thus a fairly useless object.

The caveat

However, it turns out that a weighted sum of points, only if the weights sum to zero, is independent of whatever point was picked as the origin. Such a weighted sum is called the barycentre, or the centre of mass. In the case of your room, this limited form of addition for positions (points to be precise) does exist, which can ideally put, for e.g., you, midway between your washbasket and your overfull chair for maximising the dilemma.

As you can see, kind of the whole point of affine spaces is that there is no meaningful zero-point for the entire universe. You just have to pick some arbitrary point and call it an origin, but its choice doesn’t affect anything. The tradeoff however is that the points themselves have no representation in terms of numbers. You have to resort to the associated vector space, at which point changing the origin involves changes to the components themselves.

Phew!

So that solves our problem of how to treat positions, where the answer is that positions are points in affine space and vectors can add to them, but two points can only be subtracted from one another, and no other operations are defined on points. There are some decent references for this available if you search hard enough, and some that address this in the much more general and mind-bending setting of differential geometry. This finally resolves the mess without requiring “free” and “bound”-vectors.

As for memory pointers, they are basically positions of a kind, and thus it makes sense that adding doesn’t work for them either. This is unlike temperature, where finding and using a true zero as in the Kelvin scale (or Rankine scale! there’s more than one way to skin that cat!) enables addition.

So if we now return to our original question in part 1, of adding temperature, and ask what mathematical structure represents it best, do we have an answer? Well… a relatively simple solution is to consider a 1-D affine space, or just a real line with the affine structure added. However, it seems excessive to involve a field, a vector space, and an inner-product, considering we want to talk about “scalars”! So, in our next (and final) part, we continue on our quest to pare down confusing cruft for our most basic physical quantities.